Numpyで行列の積を求めることができます。
本投稿では行列の積を求める際の計算方法についてわかりやすく解説します。
今回は難しい数式などは紹介せず、「こうやって計算できるよ」程度に紹介していきます。
同じ形状の行列の積を求める
2×2の行列と2×2の行列の積を求めます。
まずはNumPyのインポートと計算に使用する変数を記載します。
import numpy as np
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])

計算にはnp.dot()メソッドを用います。
np.dot(a, b)
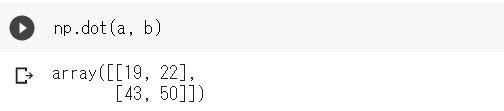
上記を式に表すと以下となります。

以下のように同じ色の枠で計算を行います。


左の行列は行ベクトル、右の行列は列ベクトルの方向で
内積(要素ごとの積と和)によって計算されます。
例えば
水色だと「1×5+2×7=19」、
黄緑色だと「1×6+2×8=22」となります。
形状が異なる行列の積を求める
2×3の行列と3×2の行列のような形状の異なる行列の積を求めます。
a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[7, 8], [9, 1], [2, 3]])
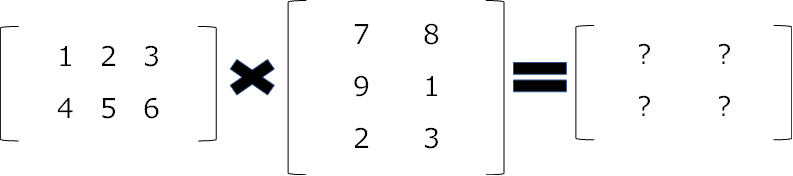
計算方法は同じ形状の行列の積の求め方と同様です。
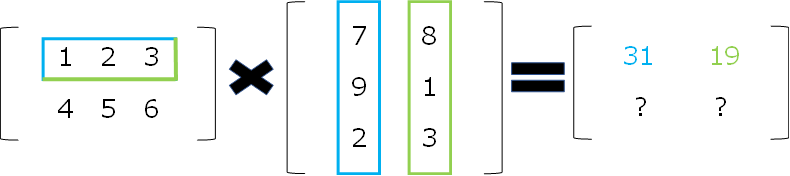
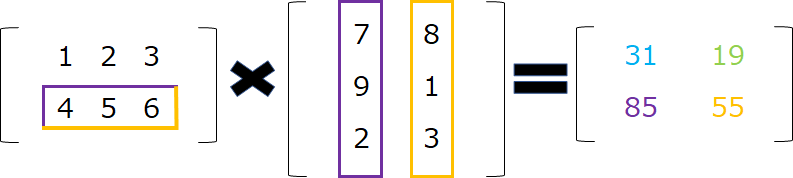
紫色は「4×7+5×9+6×2=85」、
オレンジは「4×8+5×1+6×3=55」となります。
形状が異なる行列の積を求める際の注意
形状が異なる行列の積を求めるためには満たすべき条件があります。
以下を確認してみましょう。
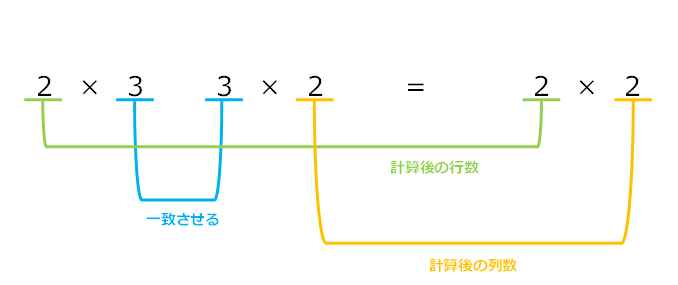
上記は「 形状が異なる行列の積を求める 」で登場した行列の形状です。
水色のラインの引いてある
左の行列の列数と右の行列の行数は必ず数を一致させる必要があります。
エラーとなる例を見てみましょう。


上記は2×3の行列と2×2の行列の積を計算しようとした際の例です。
ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)
上記のエラーメッセージが示すように
水色の枠を例に行列の積を計算しようとしても
「1×7+2×9+3×?」と右側の行列の行数が足りないため
計算することができません。
よって、左側の行列の列数と右側の行列の行数が一致した時に
2つの積を計算することができます。





コメント